I’m sure this information must be out there somewhere, but since I had a hard time finding it I figured I’d write it up in the hope that it’s useful for someone.
This is (mostly) a Test
The primary purpose of this post is to test using IPython notebooks as part of WordPress blog posts. I already did a some testing of this (see my previous post), but figured more couldn’t hurt. If someone finds it interesting, so much the better.
We transition from regular WordPress to a notebook just below:
Putting Together the Full Weather Animation
I uploaded the remaining to notebooks Animate Rainfall and Radar and Adding Sound to github.com/bitsofbits/GIS. If you are interested please take a look.
IPython Notebooks in WordPress
Animating Weather Radar Data
I’ve put up the second of four IPython Notebooks about animating weather data. It can be viewed at nbviewer.ipython.org or downloaded from github.com.
Animating Weather Station Data
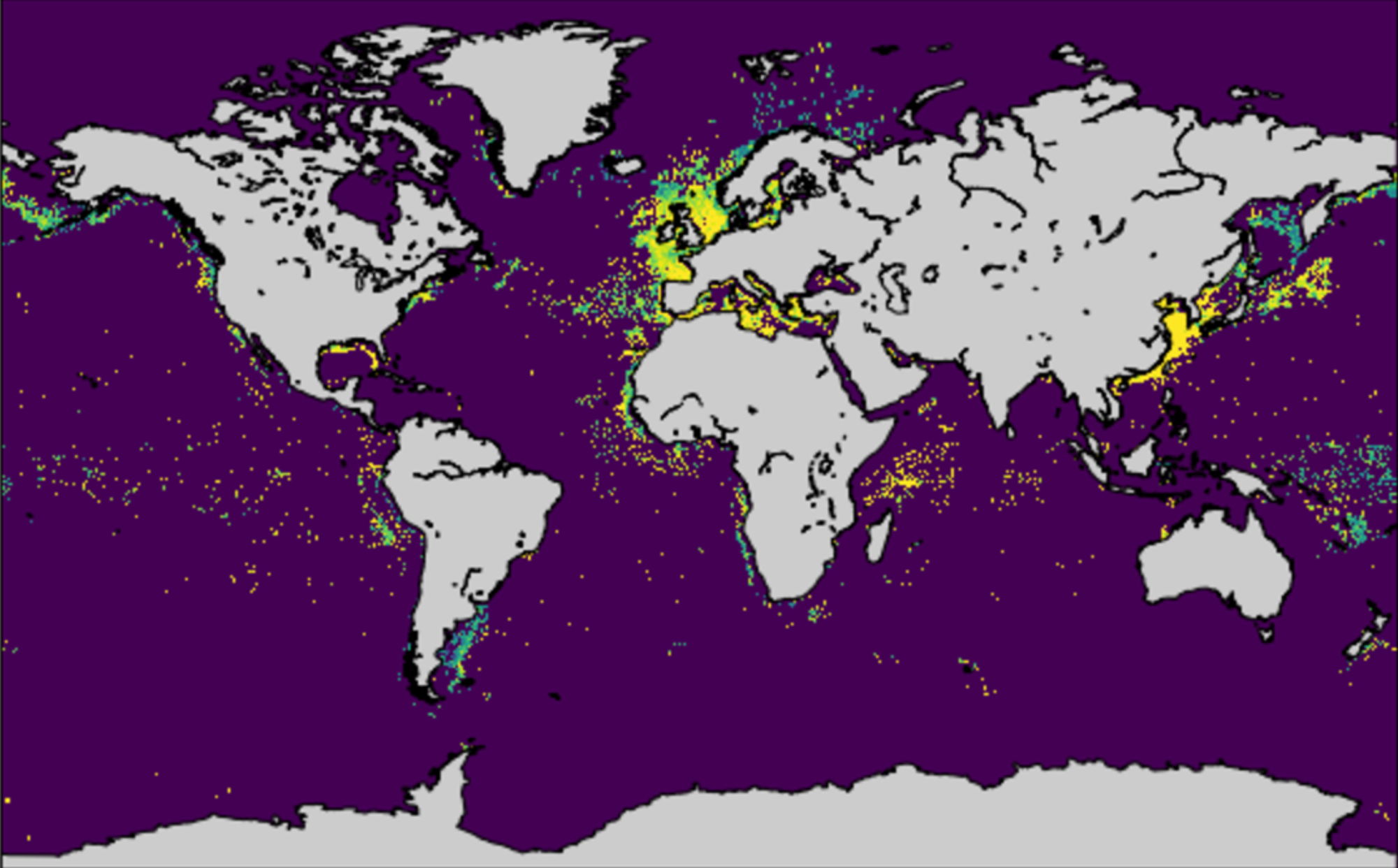
Every time there’s a big storm here, which is admittedly not that often, I think that there should be a better way to visualize the rainfall data that exists. The Flood Control District of Maricopa County maintains an extensive network of rainfall and streamflow gauges. The data is available for download, but the only forms I’ve seen it in is either as static map or as table. As a little project, I decided to download the data from the big storm we had here on September 8th, 2014 and see if I could produce an interesting animation.
Due to some prodding from friends the scope of this project crept, I ended up adding weather radar data as well as sound, and the whole thing took much longer than I’d planned on. The result is below: the blue circles are the rainfall gauges – circle area is proportional to the previous hours rainfall at that location, the red is the weather radar composite reflectivity, and the rainfall sound at a given time is proportional to the total rain at all stations1)I just add up the rainfall at all of the stations. It would be more accurate to scale the contribution of each station based local density of stations since rain in areas with more stations is overepresented in the current scheme.. The animation was produced using Python, primarily with the matplotlib package. If you are interested in how this is done, I’ve described the process of animating the just the rainfall data in an IPython notebook which can be viewed at nbviewer.ipython.org2)I just discovered this and I really like it. or downloaded from github.com. I plan to add notebooks that show how to produce the rest of the animation shortly.
References
| 1. | ↑ | I just add up the rainfall at all of the stations. It would be more accurate to scale the contribution of each station based local density of stations since rain in areas with more stations is overepresented in the current scheme. |
| 2. | ↑ | I just discovered this and I really like it. |
A Partially Successful Adventure in RPython
Before I talk about RPython, I need to say at least a little bit about PyPy. PyPy is Python interpreter, written in Python that outperforms the standard, C implementation of Python (CPython) by about a factor of six. Given that Python is generally thought to be much slower than C, one might think that was impossible. However, it is in fact faster, for most things at least, as one can see on the PyPy benchmark page.
This is possible because PyPy is only nominally written in Python. Sure, it can run (very slowly) on top of the standard CPython interpreter, but it’s really written in a restricted subset of Python referred to as RPython. The exact definition of RPython is a little vague, in fact the documentation says “RPython is everything that our translation toolchain can accept”, but essentially it removes the most dynamic and difficult to optimize portions of Python. The resulting language is static enough that the aforementioned toolchain can translate RPython code into native code resulting in a tremendous speed up. Not only that, and this is the truly amazing part, if the RPython code looks like an interpreter, it will automagically add a JIT compiler to it
That sounds impressive, but I wanted to try out the RPython toolchain to get a better feel for what is involved in translating a interpreter and how large the performance gains one could expect for straightforward, non highly tuned implementation. To this end I looked around and I found lis.py, minimal scheme interpreter written by Peter Norvig. I tried translating with this RPython and quickly discovered that this implementation is much too dynamic to be successfully translated with with RPython. So, using the basic structure of lisp.py, I rewrote the interpreter so that RPython could translate it. The result, named skeem.py (pronounced skimpy) was roughly five times longer and at least several times uglier, but did translate to a native code version named skeem-c. (This is RPython’s choice of name and I believe results from the fact that RPython first translates the Python code to C code, then compiles it).
To get an idea of the speedup, I wrote a lisp program to write out the mandelbrot set in PGM format. This will not run with the standard lis.py; I had to add a couple of commands to make generating the set feasible. Running the mandelbrot code using skeem.py takes 45,000 seconds using Python 2.7. Using PyPy it takes 532 seconds, a considerable improvement. Finally, using the translated skeem-c reduced the run time to 98 seconds. That’s a whopping 450-times improvement over the original!
Unfortunately, adding a JIT was not a success. I managed to get the skeem.py to translate with –opt=jit, but the resulting interpreter was five times slower than the interpreter without the JIT. I suspect that this is related to the main “loop” of the interpreter being recursive rather than iterative, but I didn’t dig into that.
Later, I will post some results from a second, uglier but faster, interpreter I wrote, which got a factor of two speed boost from –opt=jit.
(define x-centre -0.5) (define y-centre 0.0) (define width 4.0) (define i-max 1600) (define j-max 1200) (define n 100) (define r-max 2.0) (define colour-max 255) (define pixel-size (/ width i-max)) (define x-offset (- x-centre (* 0.5 pixel-size (+ i-max 1)))) (define y-offset (+ y-centre (* 0.5 pixel-size (+ j-max 1)))) (define (*inside? z-0 z n) (and (< (magnitude z) r-max) (or (= n 0) (*inside? z-0 (+ (* z z) z-0) (- n 1))))) (define (inside? z) (*inside? z 0 n)) (define (boolean->integer b) (if b colour-max 0)) (define (pixel i j) (boolean->integer (inside? (make-rectangular (+ x-offset (* pixel-size i)) (- y-offset (* pixel-size j)))))) (define plot (lambda () (begin (display (quote P2)) (display nl) (display i-max) (display nl) (display j-max) (display nl) (display colour-max) (display nl) (do ((j 1 (+ j 1))) ((> j j-max)) (do ((i 1 (+ i 1))) ((> i i-max)) (begin (display (pixel i j)) (display nl))))))) (plot)
[1] And, if Python in Python is six time faster, would Python in Python in Python be 36 times faster? One can only wish!
Swift Language Changes in Xcode 6 beta 3
Swift Language Changes in Xcode 6 beta 3
I noticed this a little late, but I’m happy that Apple is still tweaking Swift. Reading the manual was making me tear my hair out. This fixes one of the more egregious issues:
- The half-open range operator has been changed from .. to ..< to make it more clear alongside the … operator for closed ranges.
I still think Swift is too big though. For instance, half the closure expression syntax could go way and the language would be the better for it.
A Bit About PRBS
Pseudo random binary sequences (PRBS) show up in many applications such as cryptography and communications, but my main interest in them stems for their use in providing pseudo random data for generating eye pattern diagrams (EPD). Without getting into details on why one would want to generate EPD (see the link above for some of that), one of the issues I’ve been working on lately is how to generate PRBS at very high rates, in excess10 Gigabits per second, economically.
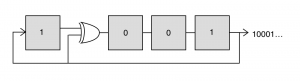
The specific type of PRBS that are used for generating EPD are the so called maximum length sequence (m-sequences) and these are typically generated using linear feedback shift register (LFSR). This is just a chain of flip-flops that is fed back on itself in a specific way to generate the PRBS of interest. To make this concrete, let’s consider a 4-bit LFSR implemented with 4 flip-flops and a xor gate as shown below. This circuit generates a repeating, length-15 series of bits: 100010011010111…
Now an important point is that these flip flips and gates tend to be relatively slow. However, serializers that convert multiple, parallel channels to a single, serial channel at a faster rate are available at quite high data rates (I’ve seen parts rated to above 50 Gbps). This suggests that a way to generate high speed PRBS is to generate multiple bits of the PRBS at a time and then combine them using a serializer. There are at least two approaches to this. One is simply to advance the sequence multiple bits at each clock. This turns out to be practical, although it requires some additional hardware. However, a more interesting, although not necessarily more practical approach, is generate alternating bits in parallel.
This second approach relies on an interesting property of these m-sequences: if one takes every other element of the sequence (this is referred to as decimation by twos), the result is a shifted sequence of the original sequence:
100010011010111100010011010111… ➡ 101011110001001… 100010011010111100010011010111… ➡ 000100110101111…
Examining these two sequences, we see that that both of the resulting sequences are just shifted versions of our original sequence, with the second sequence shifted 7 bits further than the first. With this result in hand, it’s clear that we can generate our sequence at twice the base rate if we combine two LFSR that are shifted by 7 bits with respect to each other.
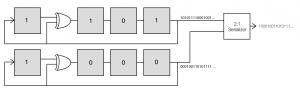
What’s particularly interesting about this is that the circuits to create the two sequences which we feed to the serializer are identical to the original LFSR except that they are initialized to different values. Furthermore, this trick can be extended to combining 4 shifted sequences using a 4:1 MUX by taking every fourth element of the original m-sequence to get shifted versions.
100010011010111100010011010111… ➡ 111100010011010… 100010011010111100010011010111… ➡ 000100110101111… 100010011010111100010011010111… ➡ 001101011110001… 100010011010111100010011010111… ➡ 010111100010011…
In fact, for longer sequences, one can take every 2nth element and always get a shifted version of the original sequence. For example, for a 10 bit LFSR, which can generate a 210-1 or 1023 bit PRBS, we could generate the sequence up to 512 bits at time using this scheme. A more realistic case would probably involve generating the sequence 64 bits at a time (this is the width of the serializers on some FPGAs). However, and this is where the possible impracticality comes in, one would need 640 flip flops as opposed to 10 flip flops for the base LFSR.
This might be acceptable in a pinch, but there is another approach that typically requires less resources. The figure shown below advances the PRBS two time steps for each clock cycle, where the two output bits can be read from the output of the two rightmost flip-flops.
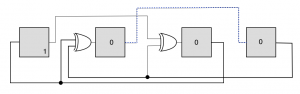
This has the same effect as the two parallel PRBS generators show above, but saves four flip flops. However, things get more complicated when generating a larger number of bits. In that case the signal needs to propagate through multiple xor gates at each clock, possibly slowing the maximum achievable data rate.
Despite the extra resources this takes up, this is an interesting way of exploiting the properties of m-sequences to generate PRBS at faster rates. It may slightly outperform the serial implementation when generating large number of bits at a time, so could be useful for generating very high rate signals. (A hybrid approach could also be envisioned where both techniques are used to reduce resources while preserving the maximum rate; interesting, but a topic for another day.)
NumPy on PyPy with a side of Psymeric
I’ve been playing around with PyPy lately (more on that later) and decided I’d take a look to see how the NumPy implementation on PyPy (NumPyPy[1]) is coming along. NumPyPy is potentially very interesting. Because the JIT can remove most of the Python overhead, more of the code can be moved to the Python level. This in turn opens up all sorts of interesting avenues for optimization, including doing the things that Numexpr does, only better. Therefore, I was very exciting when I saw this post from 2012, describing how NumPyPy was running “relatively real-world” examples over twice as fast as standard NumPy.
I downloaded and installed the NumPyPy code from https://bitbucket.org/pypy/numpy. This went smoothly except I had to spend a bit of time messing with permissions. I’m not sure if this was something I did on my end, or if the permissions of the source are odd. In either event, installation was pretty easy. I first tested the speed of NumPyPy using the micro-optimization code from last week – this was my first indication that this wasn’t going to be as impressive as I’d hoped. NumPyPy was over 10⨉ slower than standard NumPy when running this code!
I did some more digging around and found an email chain that described how the NumPyPy developers are focusing on completeness before speed. That’s understandable, but certainly isn’t as exciting as a very fast, if incomplete, version of NumPy.
I tried another, very simple, example, using timeit; in this case standard NumPy was about 7× faster than NumPyPy:
$ python -m timeit -s "import numpy as np; a = np.arange(100000.0); b=a*7" "x = a + b" 10000 loops, best of 3: 71.3 usec per loop$ pypy-2.3.1-osx64/bin/pypy -m timeit -s "import numpy as np; a = np.arange(100000.0); b=a*7" "x = a + b" 1000 loops, best of 3: 953 usec per loop
Just for fun, I dusted off Psymeric.py, a very old replacement for Numeric.array that I wrote to see what kind of performance I could get using Psyco plus Python. There is a copy of Psymeric hosted at https://bitbucket.org/dblank/pure-numpy/src, although I had to tweak that version slightly to ignore Psyco and run under both Python 2 and 3. Running the equivalent problem with Psymeric using both CPython and PyPy gives an interesting result:
python -m timeit -s "import psymeric as ps; a = ps.Array(range(100000), ps.Float64); b=a*7" "x = a + b" 10 loops, best of 3: 30.7 msec per looppypy-2.3.1-osx64/bin/pypy -m timeit -s "import psymeric as ps; a = ps.Array(range(100000), ps.Float64); b=a*7" "x = a + b" 1000 loops, best of 3: 510 usec per loop
Running with CPython this is, predictably, pretty terrible (note the units are ms in this case versus µs in the other cases). However, when run with PyPy, this actually faster than NumPyPy. Keep in mind that Psymeric is pure Python and we are just relying on PyPy’s JIT to speed it up.
These results made me suspect that NumPyPy was also written in Python, but that appears to not be quite right. It appears that the core of NumPyPy is written in the RPython, the same subset of Python the PyPy itself is written in. This allows the core to be translated into C. However, as I understand it, in order for this to work, the core needs to be part of PyPy proper, not a separate module. And that appears in fact that is the case: the core parts of numpy are contained in the module _numpy defined in the PyPy source directory micronumpy and they are imported by the NumPyPy package, which is installed separately. If all that sounds wishy-washy, it’s because I’m still very unsure on how this is working, but this is my best guess at the moment.
This puts NumPyPy in an odd position. One of main attractions of PyPy from my perspective is that it’s quite fast. However, NumPyPy is still too slow for most of the applications I’m interested in. From comments on the mailing list, it sounds like their funding sources for NumPy are more interested in completeness than speed, so the speed situation may not improve soon. I should put my time where my mouth is and figure out how to contribute to the project, but I’m not sure if I’ll have the spare cycles soon.
[1] This was a name used for NumPy on PyPy for a while. I’m not sure if it’s still considered legit, but I can’t go around writing “NumPy on PyPy” over and over.